34. Markov Chains: Irreducibility and Ergodicity
In addition to what’s in Anaconda, this lecture will need the following libraries:
!pip install quanteconOutput
Requirement already satisfied: quantecon in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (0.8.0)
Requirement already satisfied: numba>=0.49.0 in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from quantecon) (0.61.0)
Requirement already satisfied: numpy>=1.17.0 in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from quantecon) (2.1.3)
Requirement already satisfied: requests in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from quantecon) (2.32.3)
Requirement already satisfied: scipy>=1.5.0 in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from quantecon) (1.15.2)
Requirement already satisfied: sympy in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from quantecon) (1.13.3)
Requirement already satisfied: llvmlite<0.45,>=0.44.0dev0 in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from numba>=0.49.0->quantecon) (0.44.0)
Requirement already satisfied: charset-normalizer<4,>=2 in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from requests->quantecon) (3.4.1)
Requirement already satisfied: idna<4,>=2.5 in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from requests->quantecon) (3.10)
Requirement already satisfied: urllib3<3,>=1.21.1 in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from requests->quantecon) (2.3.0)
Requirement already satisfied: certifi>=2017.4.17 in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from requests->quantecon) (2025.1.31)
Requirement already satisfied: mpmath<1.4,>=1.1.0 in /opt/hostedtoolcache/Python/3.12.9/x64/lib/python3.12/site-packages (from sympy->quantecon) (1.3.0)
34.1Overview¶
This lecture continues on from our earlier lecture on Markov chains.
Specifically, we will introduce the concepts of irreducibility and ergodicity, and see how they connect to stationarity.
Irreducibility describes the ability of a Markov chain to move between any two states in the system.
Ergodicity is a sample path property that describes the behavior of the system over long periods of time.
As we will see,
- an irreducible Markov chain guarantees the existence of a unique stationary distribution, while
- an ergodic Markov chain generates time series that satisfy a version of the law of large numbers.
Together, these concepts provide a foundation for understanding the long-term behavior of Markov chains.
Let’s start with some standard imports:
import matplotlib.pyplot as plt
import quantecon as qe
import numpy as np34.2Irreducibility¶
To explain irreducibility, let’s take to be a fixed stochastic matrix.
State is called accessible (or reachable) from state if for some integer .
Two states, and , are said to communicate if and are accessible from each other.
In view of our discussion above, this means precisely that
- state can eventually be reached from state , and
- state can eventually be reached from state
The stochastic matrix is called irreducible if all states communicate; that is, if and communicate for all in .
We can also test this using QuantEcon.py’s MarkovChain class
P = [[0.9, 0.1, 0.0],
[0.4, 0.4, 0.2],
[0.1, 0.1, 0.8]]
mc = qe.MarkovChain(P, ('poor', 'middle', 'rich'))
mc.is_irreducibleTrueLet’s confirm this
P = [[1.0, 0.0, 0.0],
[0.1, 0.8, 0.1],
[0.0, 0.2, 0.8]]
mc = qe.MarkovChain(P, ('poor', 'middle', 'rich'))
mc.is_irreducibleFalseIt might be clear to you already that irreducibility is going to be important in terms of long-run outcomes.
For example, poverty is a life sentence in the second graph but not the first.
We’ll come back to this a bit later.
34.2.1Irreducibility and stationarity¶
We discussed uniqueness of stationary distributions in our earlier lecture Markov Chains: Basic Concepts.
There we stated that uniqueness holds when the transition matrix is everywhere positive.
In fact irreducibility is sufficient:
For proof, see Chapter 4 of Sargent & Stachurski (2023) or Theorem 5.2 of Häggström (2002).
34.3Ergodicity¶
Under irreducibility, yet another important result obtains:
Here
is a Markov chain with stochastic matrix and initial distribution
if and zero otherwise.
The result in theorem 4.3 is sometimes called ergodicity.
The theorem tells us that the fraction of time the chain spends at state converges to as time goes to infinity.
This gives us another way to interpret the stationary distribution (provided irreducibility holds).
Importantly, the result is valid for any choice of .
The theorem is related to the law of large numbers.
It tells us that, in some settings, the law of large numbers sometimes holds even when the sequence of random variables is not IID.
34.3.1Example: ergodicity and unemployment¶
Recall our cross-sectional interpretation of the employment/unemployment model discussed before.
Assume that and , so that irreducibility holds.
We saw that the stationary distribution is , where
In the cross-sectional interpretation, this is the fraction of people unemployed.
In view of our latest (ergodicity) result, it is also the fraction of time that a single worker can expect to spend unemployed.
Thus, in the long run, cross-sectional averages for a population and time-series averages for a given person coincide.
This is one aspect of the concept of ergodicity.
34.3.2Example: Hamilton dynamics¶
Another example is the Hamilton dynamics we discussed before.
Let be a sample path generated by these dynamics.
Let’s denote the fraction of time spent in state over the period by , so that
The graph of the Markov chain shows it is irreducible, so ergodicity holds.
Hence we expect that when is large.
The next figure shows convergence of to when and is either or 2.
P = np.array([[0.971, 0.029, 0.000],
[0.145, 0.778, 0.077],
[0.000, 0.508, 0.492]])
ts_length = 10_000
mc = qe.MarkovChain(P)
ψ_star = mc.stationary_distributions[0]
x = 1 # We study convergence to psi^*(x)
fig, ax = plt.subplots()
ax.axhline(ψ_star[x], linestyle='dashed', color='black',
label = fr'$\psi^*({x})$')
# Compute the fraction of time spent in state 0, starting from different x_0s
for x0 in range(len(P)):
X = mc.simulate(ts_length, init=x0)
p_hat = (X == x).cumsum() / np.arange(1, ts_length+1)
ax.plot(p_hat, label=fr'$\hat p_n({x})$ when $X_0 = \, {x0}$')
ax.set_xlabel('t')
ax.set_ylabel(fr'$\hat p_n({x})$')
ax.legend()
plt.show()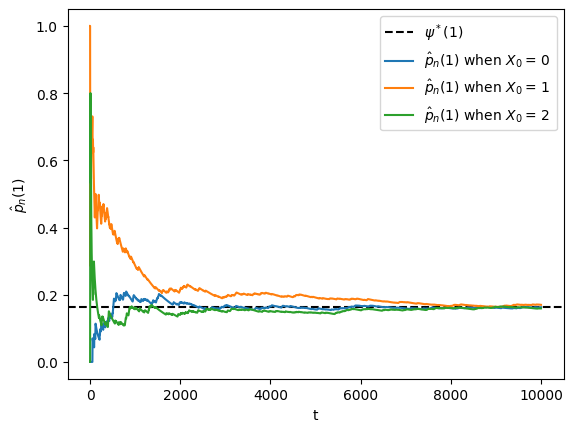
You might like to try changing to either or .
In any of these cases, ergodicity will hold.
34.3.3Example: a periodic chain¶
Not surprisingly, this property is called periodicity.
Nonetheless, the model is irreducible, so ergodicity holds.
The following figure illustrates
P = np.array([[0, 1],
[1, 0]])
ts_length = 100
mc = qe.MarkovChain(P)
n = len(P)
fig, axes = plt.subplots(nrows=1, ncols=n)
ψ_star = mc.stationary_distributions[0]
for i in range(n):
axes[i].axhline(ψ_star[i], linestyle='dashed', lw=2, color='black',
label = fr'$\psi^*({i})$')
axes[i].set_xlabel('t')
axes[i].set_ylabel(fr'$\hat p_n({i})$')
# Compute the fraction of time spent, for each x
for x0 in range(n):
# Generate time series starting at different x_0
X = mc.simulate(ts_length, init=x0)
p_hat = (X == i).cumsum() / np.arange(1, ts_length+1)
axes[i].plot(p_hat, label=fr'$x_0 = \, {x0} $')
axes[i].legend()
plt.tight_layout()
plt.show()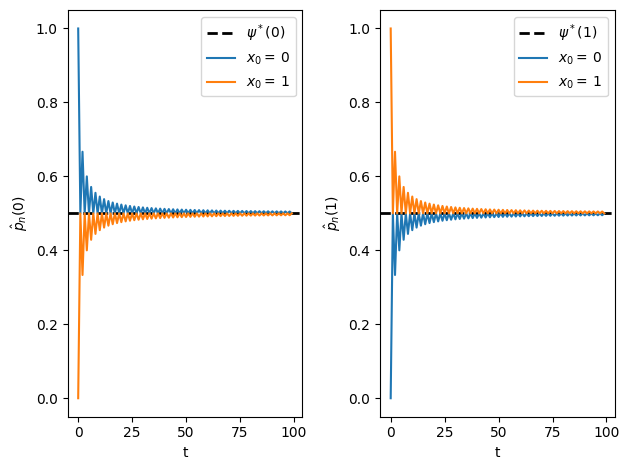
This example helps to emphasize that asymptotic stationarity is about the distribution, while ergodicity is about the sample path.
The proportion of time spent in a state can converge to the stationary distribution with periodic chains.
However, the distribution at each state does not.
34.3.4Example: political institutions¶
Let’s go back to the political institutions model with six states discussed in a previous lecture and study ergodicity.
Here’s the transition matrix.
The graph for the chain shows all states are reachable, indicating that this chain is irreducible.
In the next figure, we visualize the difference for each state .
Unlike the previous figure, is held fixed.
P = [[0.86, 0.11, 0.03, 0.00, 0.00, 0.00],
[0.52, 0.33, 0.13, 0.02, 0.00, 0.00],
[0.12, 0.03, 0.70, 0.11, 0.03, 0.01],
[0.13, 0.02, 0.35, 0.36, 0.10, 0.04],
[0.00, 0.00, 0.09, 0.11, 0.55, 0.25],
[0.00, 0.00, 0.09, 0.15, 0.26, 0.50]]
ts_length = 2500
mc = qe.MarkovChain(P)
ψ_star = mc.stationary_distributions[0]
fig, ax = plt.subplots()
X = mc.simulate(ts_length, random_state=1)
# Center the plot at 0
ax.axhline(linestyle='dashed', lw=2, color='black')
for x0 in range(len(P)):
# Calculate the fraction of time for each state
p_hat = (X == x0).cumsum() / np.arange(1, ts_length+1)
ax.plot(p_hat - ψ_star[x0], label=f'$x = {x0+1} $')
ax.set_xlabel('t')
ax.set_ylabel(r'$\hat p_n(x) - \psi^* (x)$')
ax.legend()
plt.show()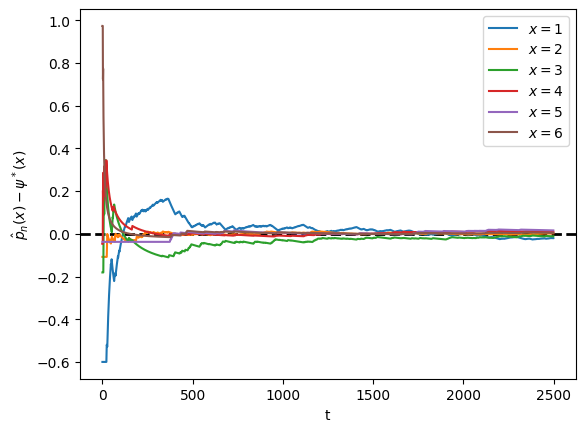
34.4Exercises¶
Solution to Exercise 1
Part 1:
One option is to take the power of the transition matrix.
P = [[0.222, 0.222, 0.215, 0.187, 0.081, 0.038, 0.029, 0.006],
[0.221, 0.22, 0.215, 0.188, 0.082, 0.039, 0.029, 0.006],
[0.207, 0.209, 0.21, 0.194, 0.09, 0.046, 0.036, 0.008],
[0.198, 0.201, 0.207, 0.198, 0.095, 0.052, 0.04, 0.009],
[0.175, 0.178, 0.197, 0.207, 0.11, 0.067, 0.054, 0.012],
[0.182, 0.184, 0.2, 0.205, 0.106, 0.062, 0.05, 0.011],
[0.123, 0.125, 0.166, 0.216, 0.141, 0.114, 0.094, 0.021],
[0.084, 0.084, 0.142, 0.228, 0.17, 0.143, 0.121, 0.028]]
P = np.array(P)
codes_B = ('1','2','3','4','5','6','7','8')
np.linalg.matrix_power(P, 10)array([[0.20254451, 0.20379879, 0.20742102, 0.19505842, 0.09287832,
0.0503871 , 0.03932382, 0.00858802],
[0.20254451, 0.20379879, 0.20742102, 0.19505842, 0.09287832,
0.0503871 , 0.03932382, 0.00858802],
[0.20254451, 0.20379879, 0.20742102, 0.19505842, 0.09287832,
0.0503871 , 0.03932382, 0.00858802],
[0.20254451, 0.20379879, 0.20742102, 0.19505842, 0.09287832,
0.0503871 , 0.03932382, 0.00858802],
[0.20254451, 0.20379879, 0.20742102, 0.19505842, 0.09287832,
0.0503871 , 0.03932382, 0.00858802],
[0.20254451, 0.20379879, 0.20742102, 0.19505842, 0.09287832,
0.0503871 , 0.03932382, 0.00858802],
[0.20254451, 0.20379879, 0.20742102, 0.19505842, 0.09287832,
0.0503871 , 0.03932382, 0.00858802],
[0.20254451, 0.20379879, 0.20742102, 0.19505842, 0.09287832,
0.0503871 , 0.03932382, 0.00858802]])For this model, rows of converge to the stationary distribution as :
mc = qe.MarkovChain(P)
ψ_star = mc.stationary_distributions[0]
ψ_stararray([0.20254451, 0.20379879, 0.20742102, 0.19505842, 0.09287832,
0.0503871 , 0.03932382, 0.00858802])Part 2:
ts_length = 1000
mc = qe.MarkovChain(P)
fig, ax = plt.subplots()
X = mc.simulate(ts_length, random_state=1)
ax.axhline(linestyle='dashed', lw=2, color='black')
for x0 in range(len(P)):
# Calculate the fraction of time for each worker
p_hat = (X == x0).cumsum() / np.arange(1, ts_length+1)
ax.plot(p_hat - ψ_star[x0], label=f'$x = {x0+1} $')
ax.set_xlabel('t')
ax.set_ylabel(r'$\hat p_n(x) - \psi^* (x)$')
ax.legend()
plt.show()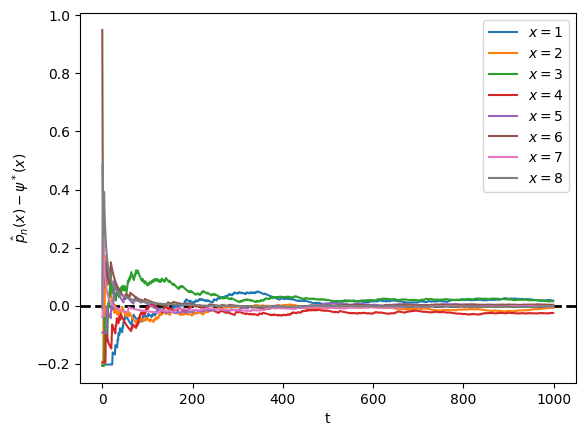
Note that the fraction of time spent at each state converges to the probability assigned to that state by the stationary distribution.
Solution to Exercise 2
We will address this exercise graphically.
The plots show the time series of for two initial conditions.
As gets large, both series converge to zero.
α = β = 0.1
ts_length = 3000
p = β / (α + β)
P = ((1 - α, α), # Careful: P and p are distinct
( β, 1 - β))
mc = qe.MarkovChain(P)
fig, ax = plt.subplots()
ax.axhline(linestyle='dashed', lw=2, color='black')
for x0 in range(len(P)):
# Generate time series for worker that starts at x0
X = mc.simulate(ts_length, init=x0)
# Compute fraction of time spent unemployed, for each n
X_bar = (X == 0).cumsum() / np.arange(1, ts_length+1)
# Plot
ax.plot(X_bar - p, label=f'$x_0 = \, {x0} $')
ax.set_xlabel('t')
ax.set_ylabel(r'$\bar X_m - \psi^* (x)$')
ax.legend()
plt.show()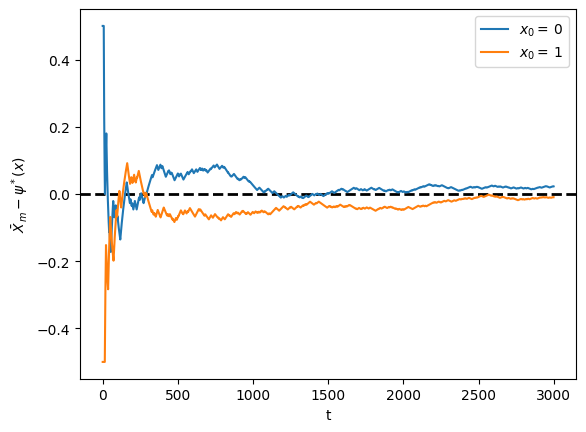
Solution to Exercise 3
def is_irreducible(P):
n = len(P)
result = np.zeros((n, n))
for i in range(n):
result += np.linalg.matrix_power(P, i)
return np.all(result > 0)Let’s try it.
P1 = np.array([[0, 1],
[1, 0]])
P2 = np.array([[1.0, 0.0, 0.0],
[0.1, 0.8, 0.1],
[0.0, 0.2, 0.8]])
P3 = np.array([[0.971, 0.029, 0.000],
[0.145, 0.778, 0.077],
[0.000, 0.508, 0.492]])
for P in (P1, P2, P3):
result = lambda P: 'irreducible' if is_irreducible(P) else 'reducible'
print(f'{P}: {result(P)}')[[0 1]
[1 0]]: irreducible
[[1. 0. 0. ]
[0.1 0.8 0.1]
[0. 0.2 0.8]]: reducible
[[0.971 0.029 0. ]
[0.145 0.778 0.077]
[0. 0.508 0.492]]: irreducible
- Sargent, T. J., & Stachurski, J. (2023). Economic Networks: Theory and Computation. arXiv Preprint arXiv:2203.11972.
- Häggström, O. (2002). Finite Markov chains and algorithmic applications (Vol. 52). Cambridge University Press.
- Benhabib, J., Bisin, A., & Luo, M. (2019). Wealth Distribution and Social Mobility in the US: A Quantitative Approach. American Economic Review, 109(5), 1623–1647.
- Zhao, D. (2012). Power Distribution and Performance Analysis for Wireless Communication Networks. Springer US. 10.1007/978-1-4614-3284-5

Creative Commons License – This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International.
